Discrete Math

Graphs

`G = (:N, A, f:)`

`N` - non-empty set of nodes
`A` - set of arcs
`f` - function that associates each arc with an unordered pair of endpoints

`G = (:{1,2,3,4,5,6}, {a,b,c,d,e}, {(a, 2-3), (b, 1-4), (c, 4-5), (d, 1-3), (e, 2-2)}:)`

Adjacent nodes - nodes that are connected by an arc.
Loop - an arc that starts and ends with the same node.
Loop free graph - graph with no loops.
Isolated node - a node not adjacent to any other node.
Degree - the number of arcs that end at a node.
Parallel arcs - two arcs with the same endpoints.
Simple - has no parallel arcs and no loops.
Complete graph - all distinct nodes are adjacent (always connected).
Path - a sequence of consecutive arcs in a graph.
Path length - the number of arcs in the path.
Connected graph - there is a path to every node in the graph.
Cycle - a path exists from a node back to the same node such that no arc is used more than once.
Acyclic - has no cycles.

Tree - a graph that is connected and acyclic (including loops).

Leaves - nodes with no children.
Internal nodes - nodes that are non-leaves.
Node depth - the length of the path from the root to the node.
Height - the greatest depth.

Node 1 is the starting node (or root node).
Node 1 is the parent node.
Nodes 2 and 3 are children of 1.
Nodes 4, 5, and 6 are children of 2.
Nodes 7 and 8 are children of 3.
a and b are branches.

A binary tree is a tree where each node has at most two children.

{"diag":{"width":"250","height":"140","elements":[{"text":{"center":{"x":127,"y":24},"text":"1","lineWidth":1,"lineStyle":"solid","lineColor":"#000000","fillColor":"#000000","fontFace":"Courier","fontHeight":10,"fontStyle":"normal","rotation":0}},{"text":{"center":{"x":26,"y":82},"text":"2","lineWidth":1,"lineStyle":"solid","lineColor":"#000000","fillColor":"#000000","fontFace":"Courier","fontHeight":10,"fontStyle":"normal","rotation":0}},{"text":{"center":{"x":219,"y":88},"text":"3","lineWidth":1,"lineStyle":"solid","lineColor":"#000000","fillColor":"#000000","fontFace":"Courier","fontHeight":10,"fontStyle":"normal","rotation":0}},{"circle":{"center":{"vertex":{"point":{"x":126,"y":40}}},"radius":4,"lineWidth":1,"lineStyle":"solid","lineColor":"#000000","fillColor":"#000000","fontFace":"Ariel","fontHeight":20,"fontStyle":"normal","rotation":0}},{"circle":{"center":{"vertex":{"point":{"x":34,"y":97}}},"radius":4,"lineWidth":1,"lineStyle":"solid","lineColor":"#000000","fillColor":"#000000","fontFace":"Ariel","fontHeight":20,"fontStyle":"normal","rotation":0}},{"circle":{"center":{"vertex":{"point":{"x":205,"y":96}}},"radius":4,"lineWidth":1,"lineStyle":"solid","lineColor":"#000000","fillColor":"#000000","fontFace":"Ariel","fontHeight":20,"fontStyle":"normal","rotation":0}},{"line":{"vertices":[{"vertex":{"point":{"x":127,"y":41}}},{"vertex":{"point":{"x":34,"y":96}}}],"lineWidth":1,"lineStyle":"solid","lineColor":"#000000","fillColor":"#ffffff","fontFace":"Ariel","fontHeight":20,"fontStyle":"normal","rotation":0}},{"line":{"vertices":[{"vertex":{"point":{"x":128,"y":42}}},{"vertex":{"point":{"x":204,"y":95}}}],"lineWidth":1,"lineStyle":"solid","lineColor":"#000000","fillColor":"#ffffff","fontFace":"Ariel","fontHeight":20,"fontStyle":"normal","rotation":0}},{"text":{"center":{"x":75,"y":60},"text":"a","lineWidth":1,"lineStyle":"solid","lineColor":"#000000","fillColor":"#000000","fontFace":"Courier","fontHeight":10,"fontStyle":"normal","rotation":0}},{"text":{"center":{"x":177,"y":61},"text":"b","lineWidth":1,"lineStyle":"solid","lineColor":"#000000","fillColor":"#000000","fontFace":"Courier","fontHeight":10,"fontStyle":"normal","rotation":0}},{"text":{"center":{"x":53,"y":113},"text":"left child","lineWidth":1,"lineStyle":"solid","lineColor":"#000000","fillColor":"#000000","fontFace":"Courier","fontHeight":10,"fontStyle":"normal","rotation":0}},{"text":{"center":{"x":203,"y":111},"text":"right child","lineWidth":1,"lineStyle":"solid","lineColor":"#000000","fillColor":"#000000","fontFace":"Courier","fontHeight":10,"fontStyle":"normal","rotation":0}}]}}

A full binary tree is a binary tree where all internal nodes have two children and all leaves of the tree are at the same depth.

Theorem - a tree with `n` nodes has `(n - 1)` arcs.

Undirected Graphs

`G = (:N, A, f :)`

`G = (:{a, b, c}, {1, 2}, {(1, a-c), (2, c-b)}:)`

This graph is described as: the set of nodes, `a`, `b` and `c`; the set of arcs, `1` and `2`; arc `1` spans nodes `a` and `c`, arc `2` spans nodes `c` and `b`.

Directed Graphs

Directed graphs are identified by a function that associates an arc with an ordered pair of nodes.

`G = (:{a, b, c}, {1, 2}, {(1, (a, c)), (2, (c, b))}:)`

This graph is described as: the set of nodes, `a`, `b` and `c`; the set of arcs, `1` and `2`; arc `1` is directed from node `a` to node `c`, arc `2` is directed from node `c` to node `b`.

Initial node - the node from which an arc begins.
Terminal node - the node where an arc ends.
Adjacent node - in a directed graph, node `b` is adjacent to node `a` if there is an arc from node `a` to node `b`.
Inverted arc - if there is an arc from node `a` to node `b`, an inverted arc would produce the opposite association from node `b` to node `a`.

Attributes of this graph:

Nodes `b` and `c` are adjacent to node `a`. Node `a` is not adjacent to nodes `b` and `c`.
Node `a` is adjacent only to node `d`.
Arc `5` is the only loop.
Arcs `2`, `3` and `4` form a cycle.
The degree of node `a` is 3; 2 arcs out, 1 arc in.

Parallel arcs - arcs that have the same initial node and same terminal node.

Complete graph - all distinct nodes are adjacent.

Connected graph - a path exists from any node to any other node.

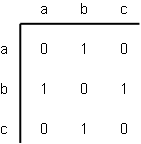
Adjacency Matrices

Adjacency matrix - the number of arcs from one node to another node.

An adjacency matrix describes which nodes in a graph are adjacent to which other nodes.

`G = (:{a, b, c}, {1, 2}, {(1, a-b), (2, b-c)}:)`

Matrix dimensions are the number of rows by the number of columns.

E.g. 2 rows X 3 columns: `[(1, 0, 1),(0, 1, 1)]`

An adjacency matrix always has the same number of rows as columns.

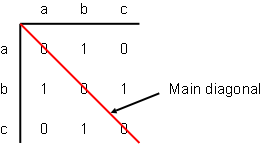
The main diagonal runs from the upper left to lower right corners of the matrix. The main diagonal will always have 0's in each position unless the graph has a loop. A loop in the graph will be indicated by a 1 on the main diagonal.

For a symmetric matrix, each side of the main diagonal is a mirror image of the other.

An undirected graph always has a symmetric adjacency matrix.

Matrix Multiplication

Square Matrix - a matrix with the same number of rows and columns.
Zero Matrix - a matrix with all zeros.

`[(0, 0, 0),(0, 0, 0)]`

Identity Matrix - a matrix with all 1'a along the main diagonal with 0's in all other positions. An identity matrix must be square.

Identity matrix: `I = [(1, 0, 0, 0), (0, 1, 0, 0), (0, 0, 1, 0), (0, 0, 0, 1)] 4 xx 4`

Not identity matrix: `[(1, 0, 0, 0), (0, 1, 0, 0)] 2 xx 4`

`I * A = A`

Matrix multiplication is NOT commutative. Order does make a difference.

`A * B != B * A`

Scalar multiplication of matrices

`2 * [(a_(11), a_(12)), (a_(21), a_(22))] = [(2 * a_(11), 2 * a_(12)), (2 * a_(21), 2 * a_(22))]`

Product of matrices

`A * B = C`

The number of columns in `A` must be the same as the number of rows in `B` to multiply.

`2xx3 * 3xx4 = 2xx4`

amath [(a_(11), a_(12)), (a_(21), a_(22))] * [(b_(11), b_(12)), (b_(21), b_(22))] = [(a_(11) * b_(11) + a_(12) * b_(21), a_(11) * b_(12) + a_(12) * b_(22)), (a_(21) * b_(11) + a_(22) * b_(21), a_(21) * b_(12) + a_(22) * b_(22))] = [(c_(11), c_(12)), (c_(21), c_(22))] endamath

Adjacency Matrices (cont.)

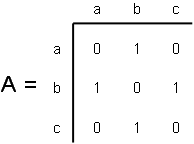
Given the following graph:

`G = (:{a, b, c}, {1, 2}, {(1, a-b), (2, b-c)}:)`

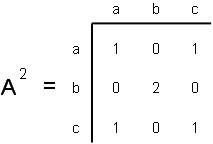
`A * A = A^2 = [(0, 1, 0), (1, 0, 1), (0, 1, 0)] * [(0, 1, 0), (1, 0, 1), (0, 1, 0)] = [(0*0+1*1+0*0, 0*1+1*0+0*1, 0*0+1*1+0*0),(1*0+0*1+1*0, 1*1+0*0+1*1, 1*0+0*1+1*0), (0*0+1*1+0*0, 0*1+1*0+0*1, 0*0+1*1+0*0)] = [(1, 0, 1), (0, 2, 0), (1, 0, 1)]`

`A` represents the number of paths of length 1.

There is one path from node `a` to node `b`.
Likewise, there is one path from node `b` to node `a`.
There is one path from node `b` to node `c`.
There is one path from node `c` to node `b`.

`A^2` represents the number of paths of length 2. There is one path of length 2 from node `a` to node `a`. The path traverses from node `a` to node `b` then back to node `a`.

There is one path of length 2 from node `c` to node `c`.
There are two paths of length 2 from node `b` to node `b`. The first traverses from node `b` to node `a` then back to node `b`. The second traverses from node `b` to node `c` then back to node `b`.
There is one path of length 2 from node `a` to node `c`. The path traverses from node `a` to node `b` then continues on to node `c`.
There is one path of length 2 from node `c` to node `a`.

`A^n` represents the number of paths of length `n` between any two nodes.

In determining the value of `n`, consider the number of distinct nodes - 1 (not including isolated nodes).

`R = A + A^2 + A^3 + … + A^n`

`R` - The number of paths `\le` length `n`

Fourth Woods Wiki

Table of Contents

Discrete Math